Более сложное изображение

Главный вопрос, связанный с использованием разрешения, состоит в правильном выборе значения разрешения. А для этого необходимо понимать, что собственно определяет конкретное значение разрешения.

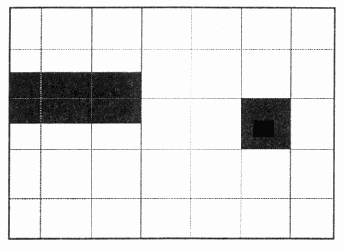
Для того чтобы в этом разобраться, стоит вместо идеального "оригинала" (черного квадрата), которым мы до сих пор оперировали, выбрать изображение не слишком сложное, но все же более близкое к жизни (рис. 8.2).

Что определяет разрешение

Один из принципиальных смысловых аспектов разрешения уже рассматривался выше.

Информацию об этом см. в разд. "Единица разрешения — ppi" данной главы.

Он заключается в определении абсолютных значений. Вводя в систему дискретизации стандартные единицы, скажем, дюйм, хотя и представляющий для российского дизайнера некоторую экзотику, мы тем самым обеспечиваем возможность единого и абсолютного измерения как на этапе дискретизации (например, в процессе сканирования), так и на этапе визуализации (например, в процессе печати на лазерном принтере).

Но, кроме этого, может представлять интерес и другой смысловой аспект ("другая сторона медали") понятия "разрешение".

Рассмотрим разрешение не с точки зрения элемента дискретизации, например пиксела как такового (его объективного размера), а с точки зрения исходного изображения, у которого тоже могут быть некоторые минимальные элементы (линии чертежа). Эти минимальные элементы, разумеется, требуют сохранения в процессе репродуцирования и отображения в конечном цифровом документе. Успешное отображение таких минимальных элементов — одно из безусловных требований сканирования штриховых изображений, которыми мы пока и занимаемся.

Дискретизация минимального элемента штрихового изображения

Рассмотрим, например, в качестве оригинала небольшой фрагмент чертежа (рис. 8.6). Характерной особенностью чертежей и довольно большого числа условных графических изображений являются линии определенной толщины, которые необходимо адекватно преобразовать в цифровое изображение ("битовую карту").

Единица разрешения — ppi

Теперь, когда было принято название элемента "пиксел", можно более точно определить понятие разрешения.

Для этого необходимо всего-навсего выбрать стандартную единицу длины, хотя в принципе, для внутреннего пользования, единица длины может быть любой: хоть пядь, хоть локоть. Однако для универсальности желательно выбрать в какой-то мере стандартную единицу.

В качестве такого стандарта принята британская мера длины — дюйм (inch), равный 25,4 мм, т. е. дюйм примерно в 2,5 раза длиннее сантиметра. Дюйм — это устаревшая, внесистемная единица измерения, однако в данной области принята в качестве стандарта и к ней уже все привыкли.

Элемент дискретизации изображений — пиксел

Квадраты — круги перед глазами. Владимир Высоцкий

Собственно, проблема состоит в том, чтобы выбрать название для обсуждаемого элемента дискретизации. Видимо, никаких подходящих слов из области искусства разработчики не нашли (или просто не знали), поэтому было придумано искусственное слово "пиксел".

Оно представляет собой просто сокращение английских слов picture element, что означает "элемент изображения", "элемент картинки". Эти два слова сократили до "pic" и "el" и соединили по принципу "колхоз", получилось слово "pixel" (при этом буква "с" заменена на "х" по причине чередования, например как в русском языке происходит чередование согласных в словах "печка" и "пекарь").

Данная глава является одной из

Глава 8.

Разрешение пиксельной графики

Данная глава является одной из центральных глав, она определяет действительно важнейший параметр — разрешение (resolution).

Для того чтобы установить единую меру дискретизации, было разработано понятие разрешения, которое однозначно связывает размер элемента дискретизации со стандартными единицами измерения, принятыми в науке и технике.

Разрешение представляет собой достаточно универсальное понятие, которое применяется в разных областях, имеющих дело с изображениями (например, в телевидении, полиграфии и компьютерной графике), оно хотя и имеет разные названия и разные формы единиц измерения, сохраняет единый смысл: количество дискретных элементов, приходящихся на стандартную единицу длины (фактически — на единицу площади).

При этом стоит обратить особое внимание на качественное содержание этого понятия, а именно уяснить, что качество, которое обеспечивается разрешением, необходимо понимать в узком метрологическом смысле: правильное разрешение должно всего лишь создать условия для передачи (отображения) минимальных элементов изображения. Это касается в первую очередь штриховых изображений, но может с оговорками распространяться и на тоновые изображения.

Отсюда возникает задача определения оптимального соотношения между размером минимального элемента оригинала и размером пиксела (критерий Котельникова—Найквиста). Неправильный выбор разрешения чреват многочисленными погрешностями, в частности неучет критерия создает условия для появления муара.

Разрешение пиксельной графики

Глава 8 Разрешение пиксельной графики Относительность размеров оригинала и оттиска Необходимость единицы измерения элементов дискретизации Понятие разрешения Элемент дискретизации изображений — пиксел Единица разрешения — ppi Более сложное изображение Что определяет разрешение Критерий дискретизации Дискретизация минимального элемента штрихового изображения Процедура измерения Округление Критерий дискретизации Расчет разрешения для штриховых изображений Муар Виды разрешения Разрешение экрана в пикселах Разрешение монитора Разрешение изображения Разрешение принтера Разрешение и линиатура Особенность битовой карты

Критерий дискретизации

А в попугаях я гораздо длиннее.
Григорий Остер

Таким образом, процедура округления состоит в определении необходимого критерия (занимает ли искомое значение положение до середины отрезка или после середины отрезка).

Исходя из вышеуказанного, можно сформулировать условие округления, а также условие любого измерения.

Для того чтобы измерять каким-либо устройством с заданной точностью, это устройство должно быть градуировано в два раза чаще. В нашем примере для измерения с точностью до сантиметров линейка должна быть градуирована рисками с интервалом в 0,5 сантиметра.

А коль скоро мы признали, что дискретизация связана с измерением самым непосредственным образом, то, следовательно, можно сформулировать и искомое условие дискретизации.

Частота дискретизации должна быть, по крайней мере, вдвое выше максимальной частоты передаваемого сигнала.

Под частотой дискретизации понимается величина, обратная разрешению, т. е. фактически — это высота пиксела. Следовательно, для того чтобы достоверно передать минимальный элемент оригинального штрихового изображения, размер пиксела должен быть меньше, как минимум, вдвое.

Критерий дискретизации

Измеряй микрометром. Отмечай мелом. Отрубай топором.

Правило точности Рэя

Качество по метрологии

Если мы используем разрешение 4 ppi, как в первом случае, или, скажем, 400 ppi, то понятно, что этим фактически определяется размер пиксела, т. е. минимальной ячейки пиксельной сетки, которая накладывается на исходное изображение ("оригинал").

Но для чего необходимо знать этот размер?

Ведь в принципе, если создана битовая карта, то в соответствии с расположением элементов в этой битовой карте изображение можно построить с помощью элементов любого размера, т. е. нам и не нужно знать размер пикселов визуализации ("какие есть — такие есть, с ними и работаем").

Муар

Задача расчета достоверной передачи минимальных элементов штрихового изображения важна еще и по другой причине.

В самом деле, ранее мы убедились, что с увеличением разрешения должно расти качество цифрового изображения. Однако необходимость уменьшения объема графического документа требует уменьшения разрешения, но при чересчур низком разрешении не только исчезают мелкие детали (это мы уже обсудили), но и возникает паразитный узор, который называется муаром (рис. 8.15).

Необходимость единицы измерения элементов дискретизации

Более простое скорее есть начало, нежели менее простое.

Аристотель

Можно предположить, что мы допустили какую-то ошибку в процессе дискретизации, и нам следует снова вернуться к начальному этапу дискретизации. Идея, может быть и правильная (выполнение повторной процедуры связано с иными установками), но предварительно необходимо решить: что мы должны изменить и в этом ли заключается проблема?

В данном случае совершенно очевидно, что причиной неоднозначной визуализации является указание только количества элементов и отсутствие каких бы то ни было указаний на размер элементов.

Но коль скоро мы говорим о соответствии размеров дискретных элементов в битовой карте и в устройстве визуализации, следовательно, мы должны эти значения "привязать" к единой шкале.

Вот это соотношение и реализуется в известном понятии "разрешение".

Округление

Как бы ни приближались друг к другу мера и измеримое, всегда между ними будет иметь место некоторое различие.

Николай Кузанский

И чтобы выразить длину объекта с принятой точностью до сантиметра, необходимо использовать процедуру округления.

Определение

Разрешение — это количество дискретных элементов в единицу длины.

До сих пор умышленно не было конкретизировано, каких именно элементов. Теперь можно их назвать.

Определение

Единица измерения разрешения ppi — это количество пикселов в каждом дюйме изображения.

Исходя из такого определения и считая, что длина квадрата, изображенного на используемом ранее "оригинале", равна одному дюйму, можно сказать,

что разрешение этого пиксельного изображения соответствует 4 ppi. Это означает, что в каждом дюйме умещается по 4 элемента (пиксела).

Описание используемого простейшего графического "оригинала" см. в главе 7.

Таким образом, введение абсолютной единицы измерения призвано обеспечивать идентичность размеров "оригинала" и "оттиска". Однако стоит рассмотреть и более сложные изображения, чтобы более глубоко разобраться в понятии "разрешение".

Особенность битовой карты

У цифровых изображений имеется важная особенность, которую необходимо понять. Суть этой особенности заключается в следующем.

Когда процесс дискретизации выполнен и получена (составлена) битовая карта, связь с оригиналом прекращается.

В самом деле, когда пользователь открывает какой-либо графический файл и рассматривает изображение, судить об этой "картинке" можно только по тому, что хранится в битовой карте.

Это цифровое изображение уже никакого отношения к оригиналу не имеет. В документе хранится только то, что было оцифровано, что превратилось в совокупность дискретных элементов. И визуализировать такое изображение можно с использованием только той информации, которая хранится в файле.

Относительность размеров оригинала и оттиска

В предыдущей главе было получено цифровое представление (битовая карта) простейшего изображения, а затем осуществлена его визуализация на экране монитора. Конечно, стоит задаться таким вопросом: обеспечиваются ли в данном случае одинаковые размеры исходного изображения ("оригинала") и конечного изображения ("оттиска")? Естественно, при обязательном условии — равенстве элементов дискретизации.

Содержание главы

Понятие разрешения

...the native hue of resolution.

William Shakespeare

(...решимости природный цвет.

пер. Михаила Лозинского)

Разрешение (resolution) является основным параметром этого вида графики.

Для более полного понимания этого параметра следует вспомнить, что мы оперируем дискретными элементами, имеющими пространственные, или точнее плоскостные, характеристики.

В самом деле, каждый дискретный элемент располагает своей собственной площадью, а все дискретные элементы заполняют общую площадь изображения. Казалось бы, соотношение между площадью этого дискретного элемента и общей площадью изображения, или общей площадью дискретизации, — как раз и должно определять такое понятие, как разрешение.

что можно на самом деле

Впрочем, не факт (мы забегаем вперед), что можно на самом деле получить адекватное качественное изображение на оттиске, даже имея "качественное битовое изображение". Надо понимать, что проблем между входом и выходом еще достаточно много.

Поэтому основное значение разрешения состоит в обеспечении качества изображения. А как следует понимать качество? Разумеется, сугубо метрологически.

Эта ситуация не настолько необычная,

Эта ситуация не настолько необычная, как может показаться на первый взгляд. Потому что конкретное печатающее устройство (принтер) располагает определенными рисующими элементами, которые не изменяются. Такую ситуацию можно сравнить с фиксированными плитками, из которых выкладывается декоративный орнамент, например на фризе здания. Из таких же "плиток", только очень маленьких, складывается изображение на экране монитора.

Это означает, что зачастую пользователь не в состоянии изменить условия вывода информации.

О проблемах конечного этапа работы с изображениями мы поговорим в части V.

В самом деле, работа с пиксельным изображением требует учета параметров на всех этапах: от оригинала до оттиска (в данном случае без кавычек).

Пример-метафора

Существует дневной снимок московской Красной площади, которая абсолютно безлюдна, что практически невозможно (там день и ночь снуют люди, туристы). Что случилось, с чем связано отсутствие людей на снимке? Причина кроется в свойстве, которое называется светочувствительностью фотопластинки. Поскольку светочувствительность данной фотопластинки была очень низкой, была установлена настолько длительная экспозиция ("выдержка", т. е. длительность открытого объектива), что на пленке оказалось зафиксированным только то, что в течение этого длительного времени было неподвижно (здания, площадь и т. д.). Объектив несколько часов стоял открытым, при этом, естественно, люди бродили и в камеру заглядывали. Движение публики, видимо, было интенсивным, и, тем не менее, это оказалось незафиксированным. Также мы не замечаем медленного изменения облаков, хотя понятно, что они непрерывно перемещаются.

Пример-метафора

Скажем, в понятие качества пищевых продуктов мы вкладываем их вкус, отсутствие вредных примесей и, наоборот, присутствие полезных ингредиентов и прочего.

Поэтому выбор разрешения и определяет взаимосвязь между оригиналом и цифровым изображением, а именно, нужно таким образом определить разрешение, чтобы цифровое изображение соответствовало исходному оригиналу.

Пример-метафора

Вам, как и компьютеру, предлагают эскиз простой мозаики, из которой следует, что нужно взять 16 элементов, 4 из которых будут черными, а остальные 12— белыми, а затем сложить из них изображение в форме "квадрата".

Совершенно очевидно, что эту задачу можно выполнить с помощью элементов различного размера и получить изображения разного размера, никак не исказив исходный эскиз.

Действительно, мы располагаем определенной таблицей (битовой картой), в которой указаны местоположение и характеристика каждого элемента. В битовой карте фиксируется размещение элементов по отношению друг к другу и "тоновое качество" элементов.

Процедура измерения

Конечно, в удаве много роста.

Но как измерить этот рост, рост, рост?

Григорий Остер

Процесс дискретизации для простоты (а, по сути, это так и есть) можно заменить известной всем процедурой измерения. Действительно, в процедуре дискретизации на "оригинал" накладывается сетка. А сетка — это ведь просто две линейки, градуированные одинаковыми единицами и расположенные перпендикулярно относительно друг друга.

Информацию о дискретизации штрихового изображения см. в главе 7.

Расчет разрешения для штриховых изображений

Приведенные выше рассуждения станут основой расчета разрешения, оптимального для передачи минимальной линии, которая имеется на штриховом изображении.

Предположим, что толщина минимальной линии, например на чертеже, составляет 2,54 мм.

Исходя из критерия Котельникова—Найквиста, высота элемента дискретизации (пиксела) должна быть в два раза меньше, следовательно,

2,54 (мм) : 2 = 1,27 (мм).

Таким образом мы получили размер одной ячейки дискретизации (пиксела), а для того чтобы получить значение разрешения, необходимо определить, сколько таких ячеек попадает в дюйм (равный 25,4 мм) в соответствии с определением понятия разрешения, отсюда

25,4 (мм) : 1,27 (мм) = 20 (пикселов).

Информацию об определении разрешения см. в главе 7.

Поскольку в каждом дюйме размещается 20 пикселов, можно утверждать, что для достоверной оцифровки штриха толщиной 2,54 мм достаточно разрешения, равного всего 20 ppi.

Разрешение экрана в пикселах

Изображение на черно-белом экране относится к пиксельной графике, потому что строится из маленьких ячеек (у телевизора эти ячейки крупнее, чем у монитора). Такая ячейка называется пиксел (pixel).

Другими словами, экран телевизора или монитора — это большая матрица, каждая ячейка которой, независимо от других, излучает определенную яркость, а все ячейки вместе отображают один кадр изображения.

В цветных телевизорах и мониторах ячейка устроена несколько сложнее (в каждой ячейке — три излучающих элемента), но принцип при этом остается прежним.

Экранная матрица монитора может быть разной размерности (в пикселах): 640x480, 800x600, 1024x768, 1152x864, 1280x1024 и 1600x1200. Поскольку сам экран физически не меняется, то при использовании видеокарты с большим разрешением размер ячейки будет меньше, а, стало быть, качество изображения — лучше (также понимаемое метрологически: более мелкая детализация).

Разрешение и линиатура

Печать полутоновых или цветных изображений возможна только с использованием технологии растрирования, которая обеспечивает преобразование уровней тона изображения в совокупность растровых точек определенного размера, которые при общем восприятии человеческим глазом сливаются и создают иллюзию непрерывного тона.

Более темным участкам изображения соответствуют более крупные растровые точки, более светлым — более мелкие (рис. 8.20). Частота растровых точек в традиционном (амплитудном) растрировании в одном изображении поддерживается неизменной и измеряется числом линий на дюйм (lines per inch — lpi). Частота растра поэтому иначе называется линиатурой растра.

Разрешение изображения

Число пикселов на единицу длины называется разрешением изображения (image resolution), и его количественной единицей считается ppi (pixels per inch — пикселов на дюйм).

Разрешение монитора

Разрешение экрана монитора определяется числом точек (пикселов) на единицу длины, обычно дюйм. Разрешение PC-совместимых мониторов не превышает 96 ppi. У изображений, предназначенных для размещения на Web-страницах, принято разрешение 72 ppi.

Программа Adobe Photoshop отображает пикселы изображения при помощи пикселов экрана (без учета физических размеров): если, предположим, разрешение документа совпадает с разрешением экрана (так стараются делать, если изображение предназначено только для экрана, например компьютерная презентация, компьютерная заставка, изображение для Web-страницы и т. д.), то изображение на экране будет отображаться "пиксел в пиксел", а это означает масштаб 100%.

Если у документа разрешение превышает экранное, то при масштабе 100% документ будет отображаться в несколько раз увеличенным (рис. 8.18). Например, изображение с разрешением 144 ppi на экране монитора будет в два раза больше, чем изображение с разрешением 72 ppi, даже если их физический размер (например, 1x1 дюйм) будет одинаковым.

Рис. 8.18. Отображение на экране изображений одинакового размера, но различного разрешения в масштабе 100%

Разрешение принтера

Разрешение принтера (в широком смысле слова) связано с количеством точек на дюйм (dots per inch — dpi), которые он может воспроизводить при печати.

Большинство лазерных принтеров имеют разрешение от 300 до 600 dpi и годятся для распечатки тоновых изображений с разрешением от 72 до 150 ppi.

Фотонаборные автоматы с разрешением 1200 dpi, 2400 dpi и выше применяются для вывода изображений с разрешением от 200 до 300 ppi и выше.

Визуализация битовой...

Рис. 8.1. Визуализация битовой карты элементами разных размеров

Исходя из этой схемы, становится очевидным, что в битовой карте отсутствует указание на реальный размер элемента. В таком случае одна и та же битовая карта может быть визуализирована по-разному, если элементы, из которых строится изображение-"оттиск", имеют различные размеры (рис. 8.1).

Оригинал более сложного изображения

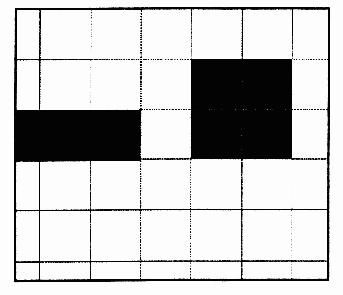
Рис. 8.2. Оригинал более сложного изображения

Особенность этого изображения состоит в несовпадении сетки дискретизации и границы между белыми и черными областями. Если мы по-прежнему станем использовать разрешение, ранее выбранное нами (4 ppi), результат визуализации оцифрованного изображения приобретет следующий вид (рис. 8.3).

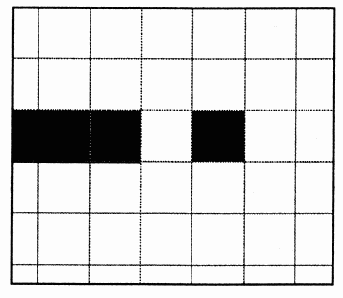
Результат визуализации с разрешением 4 ppi

Рис. 8.3. Результат визуализации с разрешением 4 ppi

Оказывается, что такое значение разрешения, которое было принято, в общем, довольно случайно и только с целью удобства (легко разбить изображение пополам и еще раз пополам), явно не обеспечивает правильного отображения. Получилось изображение, во-первых, имеющее ужасные "ступеньки", отсутствовавшие в исходном изображении, а во-вторых, оно мало похоже на исходный "оригинал". Разумеется, надо искать пути для исправления такого положения.

И вот только в этом случае вспомним, что ранее уже звучало разумное предложение вернуться к исходному состоянию, т. е. к процессу сканирования, или точнее — к этапу дискретизации. Однако давайте уточним — с какой целью? Что мы должны изменить?

Предложение вернуться к начальному этапу встречалось в главе 7.

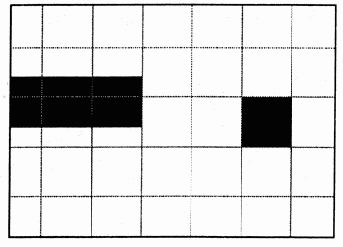
Если есть желание более адекватно передавать в цифровом дискретизиро-ванном изображении такие наклонные элементы, необходимо уменьшить размер элементов дискретизации (пикселов), а для этого, соответственно, придется увеличивать разрешение. Например, размер пикселов можно уменьшить вдвое и получить разрешение 8 ppi.

Обратите внимание, что в этом случае в визуализированном изображении (рис. 8.4) ступеньки станут в два раза меньше.

Таким образом, увеличивая разрешение (и, соответственно, уменьшая фактический размер пикселов), мы, в конце концов, сможем достичь такого уровня, когда таких ступенек не будет вовсе!

Результат визуализации с удвоенным разрешением

Рис. 8.4. Результат визуализации с удвоенным разрешением

А возможно ли такое разрешение, при котором элементы дискретизации вовсе исчезнут ("как класс")?

Разумеется, нет. Зато вполне можно достигнуть уровня, при котором эти элементы станут неразличимыми для восприятия (как, например, на фотографии).

Визуализация усложненного...

Рис. 8.5. Визуализация усложненного оригинала с соответствующим разрешением

Структура светочувствительного слоя пленки или фотобумаги предполагает, что дискретные элементы фотоизображений неоднородны, а это идеальная ситуация для адаптивного отображения тоновой картины. Дискретные элементы цифровых изображений, которые принудительно создаются, имеют принципиально (в настоящий исторический период) однородный характер.

Для того чтобы получить, в конце концов, адекватный оригиналу оттиск, пользователь должен определить соответствующее этому разрешение. С более "сложным изображением" проблема будет также решена (рис. 8.5).

Теперь настало время выяснить более детально, что же определяет величина разрешения.

Условный фрагмент чертежа

Рис. 8.6. Условный фрагмент чертежа

Если мы выберем разрешение столь же произвольно, как раньше, и высота пиксела значительно превысит толщину линии (рис. 8.7), то в этом случае необходимая исходная линия вовсе не может быть отражена в битовой карте.

Соотношение толщины линии и высоты пиксела

Рис. 8.7. Соотношение толщины линии и высоты пиксела

Это происходит потому, что сетка дискретизации, которая накладывается на изображение, просто "не увидит" этой линии.

Равные значения высоты пиксела и толщины линии

Рис. 8.8. Равные значения высоты пиксела и толщины линии

Таким образом, если высота пиксела оказывается равной (или очень близкой, т. е. в пределах погрешности) минимальному элементу изображения, то мы можем передать такую линию вполне достоверно. А так ли это?

Дело в том, что если посмотреть внимательнее, данный случай напоминает идеальную ситуацию, какая имела место при оцифровке квадрата.

Информацию об "идеальном квадрате" см. в главе 7.

На самом деле сетка дискретизации (пиксельная сетка) вряд ли так четко совпадет с линиями оригинала. Вероятнее всего, никогда не совпадет. А в таком случае возможны два основных варианта (повторяем: по-прежнему при равенстве высоты пиксела и толщины линии).

Сетка дискретизации может быть слегка сдвинута по отношению к исходной линии вверх или вниз (рис. 8.9). По правилам квантования (округления), о которых можно прочесть ниже, получается следующий результат (рис. 8.10): линия, создаваемая пикселами в битовой карте, "съезжает", соответственно, вверх или вниз на целый пиксел.

Подробную информацию о правилах квантования см. в главе 9.

Сетка дискретизации проходит строго по середине исходной линии (рис. 8.11). Если уж мы предположили, что линия сетки дискретизации проходит по краям линии, то и такой вариант возможен. По тем же правилам получается следующий результат (рис. 8.12): линия, создаваемая пикселами в битовой карте, увеличивается по толщине вдвое.

Сетка дискретизации...

Рис. 8.9. Сетка дискретизации слегка сдвинута по отношению к линии оригинала

Результат дискретизации...

Рис. 8.10. Результат дискретизации (серым цветом обозначен сдвиг)

Сетка дискретизации...

Рис. 8.11. Сетка дискретизации проходит строго по середине линии

Результат дискретизации

Рис. 8.12. Результат дискретизации

Приведенные выше результаты убеждают в том, что наш идеальный вариант (равенство размера сетки дискретизации толщине линии) далеко не идеален, как это может показаться на первый взгляд. В обоих случаях наблюдаются достаточно серьезные погрешности, которые препятствуют обеспечению достоверного качества исходного изображения.

Следовательно, необходимо внести коррективы в выбор разрешения, и единственный путь — увеличить разрешение. Но тут возникает естественный вопрос: насколько требуется увеличить разрешение?

Скажем, можно увеличить разрешение до максимального (10 000 ppi и выше). Такой вариант может оказаться очень дорогим, т. к. придется использовать совокупность очень дорогостоящего оборудования. Такое разрешение присуще только барабанным сканерам, которые "работают" только с прозрачных оригиналов, в частности со слайдов. Если требуется слайд для чертежа, даже его фрагмента, то — это слайд довольно большого размера, для обработки которого также необходимо особое профессиональное оборудование.

Исходя из этого, затраты вряд ли окажутся соизмеримыми задаче, поэтому давайте найдем условия минимизации этой задачи: насколько нужно увеличить разрешение, чтобы соблюсти экономию и решить проблему качества.

Если сформулировать эту задачу проще, необходимо определить соотношение между размером минимального элемента оригинала и размером пиксела.

Пример муара

Рис. 8.15. Пример муара

Информацию о параметрах, определяющих объем пиксельного файла, см. в главе 10.

Механизм возникновения муара состоит во взаимодействии двух сеток, разрешение которых близко друг другу. Периодическая структура изображения (минимальные периодические линии оригинала) лежит в граничной зоне (близка разрешению) дискретизации.

Муар — это одна из многих проблем, неизбежно сопровождающих процесс растеризации (рис. 8.16). Впрочем, муар — коварное явление и возникает в самых неожиданных случаях, например в результате операции изменения разрешения в сторону уменьшения (downsampling) (рис. 8.17). Это связано с тем, что растровые образцы таким образом "отвечают" на выбрасывание элементов изображения.

Муар на наклонных линиях...

Рис. 8.16. Муар на наклонных линиях, возникающий при недостаточном разрешении (центральный треугольник)

Рис. 8.17. Уменьшение разрешения вызывает появление муара

Изображения с разным разрешением

Рис. 8.19. Изображения с разным разрешением

На рис. 8.19 представлены два изображения с одинаковыми размерами, но разным разрешением. При выводе на экран изображения с меньшим разрешением, чем у экрана, программа "старается" сохранить размер изображения, поэтому для отображения каждого элемента изображения используется множество пикселов экрана.

Изображение с большим разрешением содержит больше пикселов, которые имеют меньший размер, чем у изображения с меньшим разрешением, у которого пикселы имеют больший размер.

Например, в одном квадратном дюйме изображение, предназначенное для вывода на экран монитора с разрешением 96 ppi, содержит 9216 пикселов. В том же квадратном дюйме изображение, предназначенное для вывода на лазерный принтер с разрешением 600 dpi, содержит 360 000 пикселов. Очевидно, что во втором случае физический размер пикселов будет в 70 раз меньше.

Более высокое разрешение позволяет передавать больше деталей и более точно репродуцировать оригинал. Таким образом, величина разрешения в значительной степени определяет качество цифрового изображения.

Однако следует очень четко уяснить, что уровень качества изображения закладывается в процессе сканирования в зависимости от устанавливаемого разрешения. Последующее увеличение разрешения цифрового изображения в любом графическом редакторе, в том числе и в программе Adobe Photoshop, не способствует улучшению качества изображения. Это связано с тем, что программа, конечно, не способна добавить новую изобразительную информацию (добавить новые более мелкие детали), а только перераспределить уже имеющиеся данные на большее число пикселов. В этом случае, как правило, даже происходит ухудшение некоторых параметров изображения, например резкости.

Правильный выбор величины разрешения зависит от многих факторов: назначения изображения и способа его использования. Необходимо найти разумный баланс между качеством, размером файла и временем его обработки, а также учесть возможности системы обработки.

Подробную информацию о принципах выбора параметров пиксельной графики см. в специальном разделе в конце данной части.

Фрагмент тонового изображения...

Рис. 8.20. Фрагмент тонового изображения до и после растрирования

Технология растрирования (вместе с цветоделением) представляет собой довольно сложную задачу.

Здесь же следует отметить, что качество полиграфического оттиска зависит от многих факторов, но в немалой степени от разрешения изображения и от линиатуры растра.

Соотношение между этими двумя параметрами можно в первом приближении определить эмпирической формулой: для получения оттиска полутонового изображения высокого качества следует использовать разрешение, превышающее линиатуру выводного устройства в 1,5—2 раза. Если требуется увеличение сканированного изображения, величина разрешения умножается на коэффициент масштабирования.

Следует учесть, что в любом случае необходима консультация специалистов именно того сервисного бюро или той типографии, которые будут заняты подготовкой к печати или печатью изображения.

Неизвестное изображение

Рис. 8.21. Неизвестное изображение

Поэтому решение проблемы "неверной" визуализации и несоответствия "оттиска" "оригиналу" не связано с дальнейшей обработкой битовой карты. С битовой карты взять нечего. Она такова, какова есть.

Справка

Фотографическая светочувствительность означает способность соединений серебра (галогенидов серебра) изменять свое состояние под действием света. Эта способность может быть измерена, и количественная мера такой способности называется также светочувствительностью. Точное знание светочувствительности необходимо для выбора оптимальных условий экспонирования в процессе съемки или печати.

При дискретизации штриховых изображений - аналогичный случай: в оригинале существуют линии, но коль скоро условия регистрации не соответствуют требуемым, то в этом случае они не могут быть зафиксированы.

Справка

Метрология — это наука об измерениях и методах достижения заранее определенной точности. Ее название происходит от греческих слов "metron", что означает "мера", и "logos" — "слово" или "учение". Эта наука занимается построением общей теории измерений; формированием систем единиц физических величин, разработкой методов измерений, созданием и поддержкой эталонов, проверкой мер и средств измерений. Важнейшими вехами в истории науки и технологии являются установление эталона метра (Франция, конец VIII века), а также разработка и принятие в 1960 году Международной системы единиц (СИ).

С точки зрения метрологии качество понимается как соответствие результата заранее заданному уровню. Так что, если в оригинале имеется минимальная линия определенной толщины, то метрологически качественным будет такое цифровое изображение, которое достоверно отображает эту линию.

Справка

Округление числа понимается в математике как замена его другим числом, "приближенным". У этой процедуры предусмотрены свои правила: округление производится постепенно, справа налево; когда последняя значащая цифра меньше 4, она просто отбрасывается; в том случае, если она больше 6, ближайшая слева от нее цифра увеличивается на единицу; когда она равна 5, ближайшая слева от нее цифра увеличивается на единицу, если она нечетная, или не изменяется, если она четная (правило четной цифры). Например, число "пи" (3,141592653) можно округлить до пяти цифр (3,1416), до четырех цифр (3,142) и до трех цифр (3,14). Практическое правило округления звучит проще: если округляемая цифра меньше пяти, то она заменяется нулем, а если больше или равна пяти, то дополнительно к предыдущей цифре прибавляется единица. Например, 10,24 округляется до 10,20, а 10,28 —до 10,30.

В нашем случае суть измерения состоит в том, чтобы определить целое число полных попаданий в сантиметровые отрезки. А потом область неполного попадания округлить до целого, т. е. в сторону меньшего или в сторону большего значения.

И теперь осталось только определить простой механизм, когда использовать меньшее, а когда большее значение.

Справка

Критерий назван в честь инженера американской телефонной компании AT & Т Гарри Найквиста (Nyquist), который в 1928 году опубликовал теорему, описывающую зависимость между частотой дискретизации по времени и верхней частотой спектра сигнала. Частично мы использовали без объяснения это положение в главе 6 при объяснении дискретизации аналогового сигнала.

В России соответствующую теорему принято называть теоремой Котельникова. Котельников Владимир Александрович (род. 1908), российский радиотехник, академик РАН, директор Института радиотехники и электроники РАН. Котельников знаменит трудами по совершенствованию методов радиоприема, борьбе с радиопомехами, теории потенциальной помехоустойчивости, заложил основы радиолокации Марса, Венеры и Меркурия. Без преувеличения можно сказать, что все цифровые устройства построены на основе знаменитой теоремы Котельникова.

Справка

Дюйм — традиционная английская единица, основанная на двенадцатеричной системе счисления. А между тем, с 1 января 2000 года десятичная система измерений официально заменила в Великобритании бытовавшие там традиционные меры веса, длины и объема типа фунта, унции, мили, ярда или пинты.

Англичане весьма неохотно переходят на десятичную систему мер, поменяв свои обожаемые пинты на литры, а дюймы на сантиметры. До 1971 года действовала трехуровневая недесятичная денежная система, согласно которой любой счет мог выглядеть следующим образом: "сорок четыре фунта пять шиллингов и шесть с половиной пенсов".

Таким образом, разрешение можно определить как количество пикселов в дюйме, обычно оно обозначается как ppi (читается "пи-пи-ай"), что является сокращением от словосочетания "pixels per inch" и переводится как "пикселов в каждом дюйме".

Справка

В чем принципиальная разница между дискретной структурой фотографии и дискретной структурой компьютерной графики? Откуда берется дискретная структура на фотографии (или на слайде)?

Дискретная структура фотоизображений задается уже в процессе создания пленки или фотобумаги (ни фотоаппараты, ни увеличители не влияют на это), она только слегка изменяется в процессе экспонирования и проявки. Состав, который наносится на пленку или на бумагу, содержит галогениды серебра в виде так называемых "зерен". Их размер, изменяемый в процессе обработки, как раз и определяет элементы изображения. Исходя из этого, пленки бывают крупнозернистыми или мелкозернистыми (последние используются в полиграфическом производстве для получения фотоформ).

Особенностью дискретной структуры фотоизображений является то, что элементы дискретизации неоднородны. В процессе экспонирования и обработки отдельные зерна сливаются, создавая конгломераты различных размеров, в том числе даже видимые невооруженным глазом (особенно это заметно при очень сильном увеличении фрагмента фотографии).

Важная мысль

В метрологии качество понимается формально: как соответствие результата заранее заданному уровню.

Разумеется, если известно значение толщины минимального элемента оригинала, можно рассчитать соответствующее разрешение (создать соответствующую сетку дискретизации) и, тем самым, определить требуемый размер пиксела.

Также логично предположить, что если мы так рассчитаем разрешение, что размер стороны пиксела (не забываем, Что пиксел — это "квадратик") будет равен толщине линии, нам удастся однозначно оцифровать такой чертеж (рис. 8.8).

Важная мысль

Соотношение между размером минимального элемента и размером пиксела должно быть оптимальным: обеспечивать требуемое качество изображения и не увеличивать чрезмерно объем документа.

Исходя из этой задачи, посмотрим на процесс дискретизации с другой (более простой) точки зрения.

Важная мысль

Частота дискретизации должна быть, по крайней мере, вдвое выше максимальной частоты передаваемого сигнала, подвергаемого дискретизации.

Такая зависимость известна в западных странах как критерий Найквиста, а в России — как теорема Котельникова.

Важная мысль

Это очень важный момент: понять, что после дискретизации, квантования и кодирования, т. е. после получения цифрового изображения (битовой карты) отношения между "оригиналом" и цифровым изображением прекращаются.

Из этого проистекает важнейшее следствие: после того как мы дискретизи-ровали изображение, в битовой карте новой информации никогда не появится. Просто ей неоткуда взяться.

И если вид оцифрованного изображения по какой-либо причине вас не устраивает, а это бывает довольно часто (цифровой "квадрат" нас вполне устраивал, а цифровой "треугольник" — нет), следует возвратиться к началу процесса, т. е. к "сканированию" с другими (более подходящими) параметрами.

В этом кроется самая крупная проблема цифрового вида графики — зависимость пиксельного изображения от начального этапа работы.

Важная мысль

Следует понять: решением несоответствия "оттиска" "оригиналу" является возврат к начальному этапу работы. Все изменения полученного пиксельного изображения объективно связаны только с его искажением, хотя субъективно изображение может казаться улучшенным.

Последняя мысль служит основанием для тоновой и цветовой коррекции, речь о которой пойдет ниже.

Тоновой коррекции полностью посвящена часть VII данной книги.

Резюме

Разрешение (resolution) является основным параметром этого вида графики — пиксельной графики.
Для унификации значения разрешение разумно привести к стандартной площади. Для удобства (меньшего значения) разумнее использовать вместо единиц площади линейные единицы.
Разрешение — это количество дискретных элементов в единицу длины.
Единица измерения разрешения ppi — количество пикселов в каждом дюйме изображения.
При определенных значениях разрешения дискретная структура изображений неразличима (или почти неразличима) глазом.
Разрешение определяет абсолютное значение дискретного элемента и соответствует минимальному элементу изображения (но не оригинала!).
Частота дискретизации должна быть, по крайней мере, вдвое выше максимальной частоты дискретизируемого передаваемого сигнала.
Формула, позволяющая "прикинуть" требуемое разрешение (толщина штриха измеряется в миллиметрах):

R = 25,4 : (L : 2).

Механизм возникновения муара состоит во взаимодействии двух сеток, разрешение которых близко друг другу.
Когда процесс дискретизации выполнен и получена битовая карта, связь с оригиналом прекращается навсегда (грустный вывод).

Помимо разрешения, следующим важнейшим параметром пиксельной графики является глубина цвета.

Важная мысль

Для унификации значения разрешение разумно привести к стандартной площади.

С другой стороны, поскольку элемент дискретизации имеет квадратную форму и стандартная площадь дискретизации тоже имеет квадратную форму, это означает, что дискретизация происходит одинаково вдоль горизонтали и вертикали. Исходя из этого, удобнее принять вместо двумерной системы одномерную, т. е. линейную.

Важная мысль

Для удобства разумнее использовать вместо единиц площади линейные единицы.

Поэтому, принимая во внимание эти соображения, можно в итоге дать следующее определение понятию "разрешение".

Важная мысль

Любое изображение пиксельной (битовой, растровой) графики — это мозаика, составленная из пикселов.

Главным отличительным свойством пиксела является его однородность и неделимость. Внутри пиксела уже не может быть никаких более мелких элементов. Это как некий "атом". В каждый данный момент он такой, какой есть.

Важная мысль

Отличительными особенностями пиксела являются его однородность (все пикселы по размеру одинаковы) и неделимость (пиксел не содержит более мелких пикселов).

Осталось только соединить понятия "разрешение" и "пиксел" в единицу измерения.

Важная мысль

Действительно, при определенных значениях разрешения дискретная структура неразличима (или почти неразличима) глазом. На этом, вообще говоря, построены все технические системы, работающие с изображением (кино, телевидение, фотография и полиграфия).

На самом деле, достаточно "вооружить" глаз каким-нибудь оптическим прибором, даже несложным, и можно заметить, что всюду присутствуют некие дискретные элементы, даже если мы рассматриваем фотографию и нам кажется, что изображение и тоновая шкала непрерывны.

Важная мысль

Для штриховых изображений необходимо обеспечить достоверное отображение минимальных элементов оригинала.

Отсюда возникает задача сформулировать определенную зависимость между размером минимального элемента "оригинала" и разрешением (то есть фак-

тическим размером пиксела), но прежде необходимо понять смысл "качества цифровых изображений".

Важная мысль

Работа с пиксельным (точечным) изображением требует учета параметров на всех этапах: от оригинала до оттиска.

Но с другой стороны, почему так важно знать размер минимальных элементов — пикселов? Потому что, помимо выхода (этапа визуализации), существуют и проблемы входа (соответствия битовой карты цифрового избражения исходному оригиналу).

Виды разрешения

При рассмотрении средств дискретной визуализации можно определить несколько базовых дискретных элементов: образцов, пикселов, точек и линий.

На таких условиях строятся многочисленные

На таких условиях строятся многочисленные приемы художественной фотографии, а также компьютерной графики.

Рассматривая этот случай, мы приходим к мысли, что в понятие разрешения входит и определенная качественная сторона дела. До сих пор мы говорили только о количественной.

Вы помните, что сначала не получилось "более сложное изображение", соответствующее оригиналу.

Информацию об этом см. в разд. "Более сложное изображение" данной главы.

А теперь не получаются линии, имеющие место в оригинале.

Таким образом, действительно в понятие разрешения входит качественная составляющая (в чем мы еще не один раз сможем убедиться). Но можем ли мы этой качественной составляющей дать точное определение?

в курсе, что никакое измерение

Надеемся, читатель в курсе, что никакое измерение никогда не бывает абсолютно точным (это является основополагающим тезисом метрологии). Ибо если мы будем бесконечно увеличивать точность, то, в конце концов, придется использовать все более мелкие единицы измерения, например микроны, и все более сложное оборудование. Усложняя эту процедуру, мы обнаружим, что на молекулярном уровне потеряли границу измеряемого объекта.

Поэтому любое измерение всегда выполняется с определенной, причем заранее заданной, точностью. Например, для определенных практических целей бывает необходима точность до микрона, до миллиметра, до метра, до километра и т. д.

в общем случае является философским.

Вопрос о точности в общем случае является философским. Можно ли утверждать что-либо истинным, если абсолютно точных измерений не бывает. Любое измерение, а следовательно, и любое репродуцирование, неизбежно основанное на измерении, не может быть "истинным", т. е. абсолютно адекватным "оригиналу". Практическая задача заключается только в том, чтобы обеспечить тот уровень, который заранее устанавливается и на который способны технология и технические системы.

Это значит: если мы берем школьную линейку, то понятно, что с ее помощью измерить с точностью до микрона невозможно. Если в самом деле требуется такая точность, нужно брать соответствующий инструмент измерения и отдавать себе отчет в предстоящих трудностях технического и финансового порядка.

Предположим, нам необходимо измерить условный объект с точностью до сантиметра. Для этой цели мы используем линейку, градуированную в сантиметрах (рис. 8.13).

На рисунке заметно, что граница объекта располагается между значениями "4" и "5".

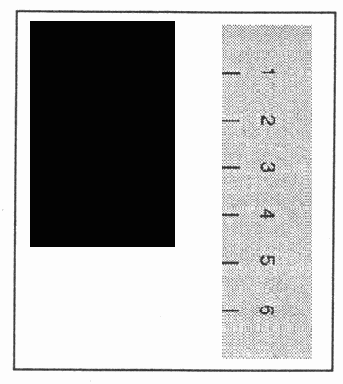
Рис. 8.13. Условный объект, предназначенный для измерения, и линейка

обычно предлагают разбить сантиметр на

На лекциях дизайнеры, в отличие от "технарей", обычно предлагают разбить сантиметр на миллиметры, т. е. на 10 частей, как это и имеет место на реальных линейках. Разумеется, в этом предложении нет ничего абсурдного, но вместе с тем есть избыточность от непонимания логики ситуации. Предположим, мы разбиваем на миллиметры. В этом случае, если количество миллиметров будет больше 6, то в соответствии с правилом округления, мы запишем большее значение, а если меньше 4, то, в соответствии с тем же правилом, — меньшее.

Но нужна ли такая точность (и почему на 10 частей, а не на 100), если в действительности нам необходимо только понять, располагается край измеряемого объекта до середины неполного сантиметра или после середины? Значит, действительно, нам на самом деле достаточно в этой ситуации середины.

Таким образом, при наличии центральной риски мы вполне достоверно можем сказать, что, если край объекта располагается за этой риской, то, значит, длина объекта с точностью до сантиметра равна "5 сантиметрам" (рис. 8.14), а если до этой риски — то "4 сантиметрам".

Рис. 8.14. Условия, необходимые для измерения с точностью до сантиметра

что здесь представлен довольно условный

Разумеется, что здесь представлен довольно условный пример, с удобными числами для расчета.

Возьмем более сложный пример. Скажем, толщина линии составляет половину пункта (пункт равен 1,72 дюйма), т. е. толщина линии равна примерно 0,176 мм.

Попробуем свести наши расчеты в одно уравнение:

25,4 (мм) : (0,176 : 2) = 288 (пикселов),

что также означает разрешение 288 ppi, которое весьма часто используется в дизайнерской практике.

Суммируя примеры, можно вывести общую формулу, позволяющую "прикинуть" требуемое разрешение, если мы обозначим толщину минимального штриха буквой L (толщина штриха измеряется в миллиметрах), а разрешение — буквой R. Итак,

R = 25,4 (мм) : (L : 2).

Если толщина штриха измеряется в дюймах, формула будет еще проще:

R = 1 : (L : 2).

когда мы получили такое изображение

Действительно, когда мы получили такое изображение (рис. 8.21), что мы можем сказать об этом изображении? Откуда мы можем знать, что служило в качестве "оригинала"? Действительно, мы не знаем, если не видели оригинала!

о том, что необходимо вернуться

Идея о том, что необходимо вернуться к этапу дискретизации и изменить параметры данного процесса, не лишена оснований. Эта мысль еще нам пригодится.

О причинах возвращения к начальному этапу дискретизации с другими параметрами с/и. в разд. "Более сложное изображение" данной главы.

Именно такое разрешение характерно для

Именно такое разрешение характерно для устройств с фиксированным количеством элементов дискретизации, например экран монитора. Считается, что стандартное разрешение монитора 800x600. При этом понятно, что размеры элементов в мониторах, размер которых — 14x21 дюйм, будут различными. В областях графики, ориентированных только для экранного представления, скажем, изображения для Web-страниц, такое представление разрешения гораздо удобнее.

Логически это допустимо, но вместе с тем заметно некоторое неудобство, причем двух типов.

С одной стороны, достаточно сложно всякий раз вычислять соотношение количества всех элементов дискретизации и общей площади дискретизации (тем более, что вряд ли будут получаться "удобные" целые значения). Разумнее привести это к стандартной площади, например квадратному сантиметру, квадратному дюйму или любой другой принятой в качестве стандартной единице измерения.

в русском языке слово встречается

Единственная трудность: в русском языке слово встречается в двух вариантах — "пиксел" и "пиксель". В английском языке этой проблемы нет, поскольку язык не располагает палатализацией (смягчением согласных звуков).

Мы лично склоняемся к твердому варианту — "пиксел", все-таки звучит ближе к английскому и более солидно. Но, впрочем, не настаиваем. Кому хочется мягкости, могут использовать другой вариант. Тем не менее в литературе все-таки чаще встречается написание "пиксел".

Таким образом, пиксельная графика, или битовая графика, т. е. та таблица, которая хранится в компьютере (в оперативной памяти или на диске), представляет собой совокупность пикселов, можно даже сказать, мозаику пикселов.

и важно, поскольку, если потребуется,

Впрочем, это не столь и важно, поскольку, если потребуется, мы можем этот стандарт привязать к международной системе измерения единиц СИ, в которой, кстати, отсутствуют миллиметры, там приняты только метры. Однако графическим дизайнерам неудобно использовать метры, поскольку это довольно значительная величина. Но вот миллиметры их вполне бы устроили, поскольку известно, что формат бумаги может измеряться в миллиметрах и т. д. Но раз уж решили, так решили...